Endless waterfall ... return Universe © copyright 1998 Wayne Roberts All rights reserved.
transparent watercolour on Arches paper, collection J & J Poole. Use scroll-bar to see commentary below image.
In Internet Explorer, press F-11 key (on the top row of your keyboard) to maximise image-area on screen.
Press F-11 key again to return to full tool-bar view in IE4+ & normal window    Home | closer view ideal for 1152 x 864px. See also new web site published October, 2004, presenting a new art-science-math-music theory, culmination of 10 years freelance work by the artist/author, Wayne Roberts.

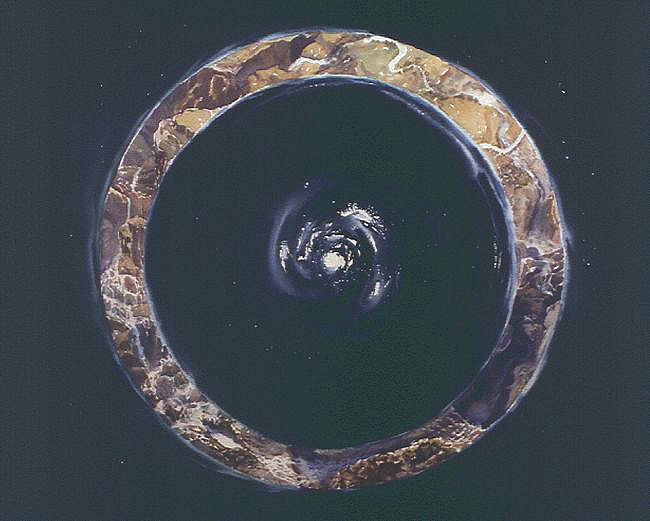
Start looking inside the ring at the 12 o'clock position and follow anti-clockwise. You'll see a river running through a canyon, and then at 10 o'clock it starts to drop into a waterfall. Your view gradually becomes 'aerial', and at six o'oclock you're looking straight down on the falls from above, as it drops into successive canyons. At two o'clock there is a road-bridge across the river and your view is more skewed even though still from above. From here the water returns mysteriously to its source having 'fallen uphill'.

In this composition, there is a 'half-twist' in the viewer's perspective as one proceeds to 'sequentially observe or follow' the circumference of the circle, much like that of the renowned Moebius band of mathematics. This twist, instead of existing in the solid or at the surface, exists in the space ' in between' the observer and the surface observed.

Escher constructed a very clever drawing of an 'impossible waterfall' and made it all the more astonishing by convincing us that his 'perpetual motion' machine which seems to our surveying eyes entirely logical, could even power a turbine! His perspectival 'twist' was inspired by the Penrose tribar (a kind of impossible three-dimensional triangle).

If we regard mathematical illusions and the 'logic of the impossible' as 'mere curiosities', and 'quaint tricks', we should not forget the lessons of history. Such lessons may change our view. For example, whilst it is true that parallel lines do not meet in the (Euclidean) geometry of the flat plane, there are equally valid (consistent) geometries of curved-surfaces (non-Euclidean) in which 'parallels' do in fact meet, and in other cases, diverge. Einstein utilised these ideas to help him formulate his General Theory of Relativity, in which he proposed that matter 'bends' (changes the curvature) of the 4-dimensional space-time 'surface'. This was a new and radical way of accounting for the effects of 'gravitation'. In a bizarre twist, he proposed the idea that planets, stars, etc are actually travelling along 'straight lines' (called geodesics) on this 'twisting surface', that is, they follow the 'shortest, most-direct, path' through space-time. By way of analogy, consider a ship's course across the ocean: for its captain, it is taking a direct ('straight line') course from one port to another at a distant point, on the other side of the ocean. But to an observer from space, the ship's course is seen to follow the curvature of the Earth's surface. It's path is the shortest distance between two points, but on a curved surface (i.e. a geodesic). In this sense it is both straight and curved. Or consider a velodrome: cyclists can, at appropriate speed, travel around the tight curves without turning the front wheel, by virtue of the steep camber (the slope of the curve). They steer a straight line, but the curvature of the surface makes them turn. These ideas are 'paralleled' in the painting.

The painting echoes another concern. That is that what seems to be so real, such as the linear passage of time, may in fact be a lower-dimensional illusion of our minds. Twentieth century physics affirms this. If we could perceive space-time from a higher-dimensional viewpoint, we might observe (figuratively) something like this: a strange and beautiful 'convoluting connectedness', without any 'loose ends'. An ocean of connectedness, of 'waves' that rhythmically ebb and flow, rise and fall, and whose peculiar unique forms are determined not by a static predetermined monotonous metric, but by a liquid poem whose rhyme and meter only emerges from the symphony of all the lines, and all of the verses, stunningly measured, but whose measure both stretches and shrinks, twists and turns, yet remains forever balanced, even in the cusp, ...every point, every entity, taking its cue from every other, ...every syllable included in the rhyme and meter, every line, every stanza, ...even the boundaries of stanzas rippling through the whole such that each syllable in turn shares in the beginning and the end, of line, of verse, of poem.

Further-enlarged view, 165Kb

home | return to thumnail of this painting | the discreteness of infinity | other paintings | links | contact | awards | mod figurative | seascapes | mountains in watercolour | general watercolours | generic landscapes
related work | a new way of painting light